[AD] 運営維持のため、一部広告リンクを設置する場合がございます(詳細)
投資では、「ボラティリティ」という言葉が頻繁に使われますが、皆さんは正しくその意味や見方を理解していますでしょうか?
FXにおいては「ボラティリティ=値動きの大きさ」といった捉え方になりますが、ボラティリティとは、将来的な変動を予想するための重要な指標でもあるのです。
本記事では、そんなボラティリティについて詳しく解説していきますので、ぜひ参考にしてみてください。
目次
インプライドボラティリティとは?

そもそもボラティリティって?
ボラティリティとは、金融資産の変動率の大きさを意味します。
よく株式投資やFXにおいて、「ボラティリティが大きい」といった言葉が使われたりしますが、これは相場の値動きが活発になっている状態です。
またボラティリティを算出する方法は2パターンあり、それが「ヒストリカルボラティリティ」と「インプライドボラティリティ」と呼ばれるものです。
ヒストリカルボラティリティとインプライドボラティリティ
ヒストリカルボラティリティとは、過去のデータに基づいて、統計的に算出したボラティリティです。
MT4やTradingview等のチャートツールにおいては、ヒストリカルボラティリティを用いたインジケーターが数多く搭載されており、有名な「ボリンジャーバンド」もそのうちの1つです。
一方インプライドボラティリティとは、現在の状態から、将来的な変動率を予測するためのボラティリティ。
価格変動に対する将来的な期待度や、市場参加者の需給が反映されているため、今後の値動きを予想する際は、このインプライドボラティリティが重視されます。
オプション取引とは?
オプション取引とは、一定の期間内にあらかじめ決められた数量を、あらかじめ決められた価格で、受け渡しする「権利」を「売買」する取引です。
 ノックアウト・オプションとは?メリット・デメリットは?始め方も解説
ノックアウト・オプションとは?メリット・デメリットは?始め方も解説
例えば、米ドル円を10Lot(10万通貨)ほどロングポジションで保有したい、そんな状況を例に考えていきましょう。
現在のレートは1米ドル=110円。10Lot保有するためには、レバレッジを25倍適用させても、44万円の資金が必要になります。
ただ現在は持ち合わせがなく、資金の目処がつくのは6ヵ月後。その頃には米ドル円のレートはさらに上昇しているかもしれません。
とはいえ、10Lotを44万円で保有するという契約を結ぶわけにはいきません。なぜなら6ヵ月後の為替レートが、110円から大きく下げていた場合こちらが損をしてしまうからです。
そこで思いついたのが「6ヵ月後に44万円で、米ドル円ロングを10Lot保有できる権利」。
この権利を買っておけば、10Lotを44万円で保有することもできるし、権利を放棄してもOKです。
6ヵ月後に米ドル円のレートが115円になっていれば、本来10Lot保有するのに46万円必要なところ44万円で保有することができ、その差額分を儲けとすることができます。
以上がオプション取引の簡単な仕組み説明となります。
本記事では、以後オプション取引に関連した話が続きますが、「オプション取引=現状の取引条件を先延ばしにできる権利」と捉えておくと、わかりやすくイメージできるのではないでしょうか。
理論価格とは?
理論価格とは、特定の変数(原資産価格・権利行使価格・金利・残存期間・原資産のボラティリティ)から算出されるオプション価格を意味します。
またオプション価格とは、オプション取引の買い手が、売り手に対して支払う金額のことです。
なぜ、ここで理論価格(オプション価格)について取り上げているのかと言えば、理論価格は、オプション取引を有利に進めるための知識の1つだからです。
とはいえ理論価格についての説明は、どの記事を読んでも分かりにくく、初学者の方にとっては厄介に感じてしまうかも知れません。
そこで超ざっくりと言えば、理論価格とは、
「様々な条件を考慮すると、理論的には、このぐらいのオプション価格になるだろう。」
といった認識を持っていただければOKです!
ボラティリティで理論価格が決まる
前節で紹介した理論価格は、ボラティリティによっても大きく左右されます。
本来ボラティリティが大きくなると、将来的な予測が立てづらく、今後どうなっていくのか見通しが立ちません。
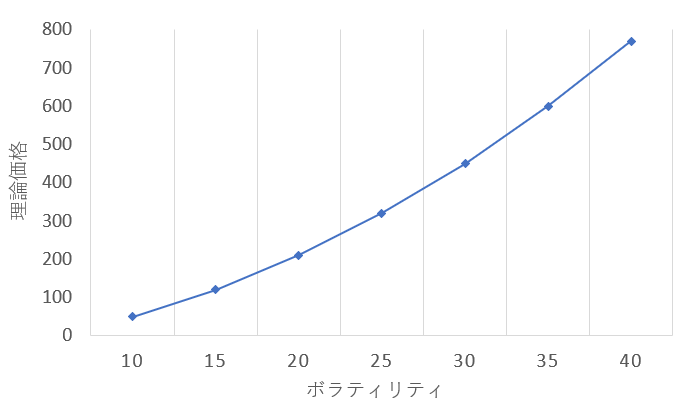
そのためオプション取引においては、ボラティリティが高くなるほど理論価格(=オプション価格)も高いとされ、逆にボラティリティが低いほどオプション価格も低くなります。
このポイントを念頭に置いて、オプション取引に挑む際は、相場が比較的落ち着いた状況を選ぶべきといえるでしょう。
理論価格の計算方法
理論価格は、ブラックショールズ方程式によって算出することができます。
この方程式は、1997年にノーベル経済学賞を受賞したショールズ氏とマートン氏によって考案され、現在も世界中の金融機関に実用されるほど、現代に与える影響は大きいです。
一般的にブラックショールズ方程式は、以下の計算式で表記されます。
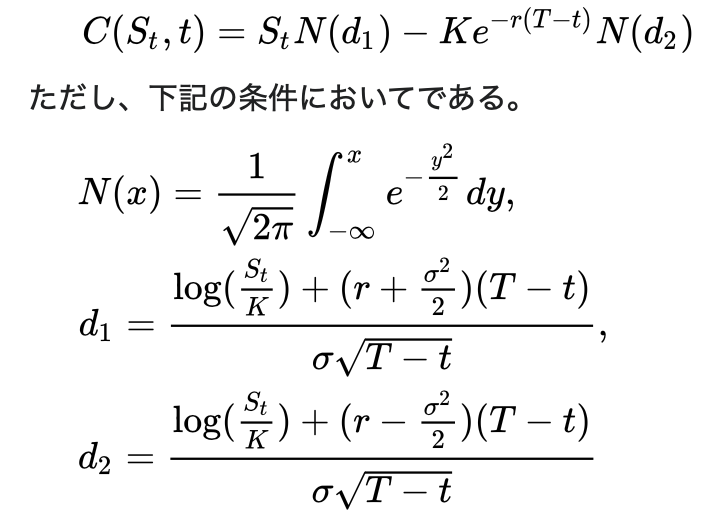
一見すると複雑な計算式であるため、理解するのが非常に難しく感じるかもしれません。
しかし行なっていることは実に有用で、「原資産価格」「権利行使価格」「ボラティリティ」「残存期間」「金利」「配当利回り」、これらを考慮してオプションの理論価格を算出するというもの。
最近では、上記の方程式を反映したエクセルフォーマットもネット上で公開されており、必要なパラメータがあれば、誰でも計算できるようになっています。
最も重要なのはリスク管理

あらゆる投資において、リスク管理の重要性は共通しています。
稼げる手法ばかりに目を向けるのではなく、どうすればお金を守れるのか…本節ではその指標となるリスクファクターを5つほど紹介していきます。
デルタ
最も意識しておくべきリスクファクターが、デルタです。
計算式:デルタ = オプション価格の変化額 ÷ 原資産価格の変化額
では、このデルタが具体的にどう役立つのか…?
仮にデルタの値が「0.5」、またオプション取引と表示されている状況を考えてみましょう。
この時、ドル円が100から110円まで変動した時、オプション価格は5円(= 10円 × 0.5)変動することになります。
デルタの値は、0から1までの絶対値で示されますが、1に近づくほど、オプション価格が高くなる可能性が高いということです。
ガンマ
ガンマは、上述したデルタがどれだけ変化するかを表す指標です。
計算式:ガンマ = デルタ値の変化幅 ÷ 原資産価格の変化額
ガンマの値が大きくなるほど、原資産価格が変動した時のデルタの値の変化も大きくなる、つまりオプション価格も高くなりやすいということです。
また逆に、ガンマが小さくなるほどデルタの変化は小さくなるため、オプション価格を抑えやすくなります。
セータ
セータは、満期までの残存日数の減少により、オプション価格がどれだけ減少するのかを示した指標です。
計算式:セータ=オプション価格の変化額 ÷ 残存日数の減少
一般的に、取引の残存期間が短くなるほど、時間的価値の減少が大きくなります。
つまりセータの値が大きいほど、残存日数が1日減少したときのオプション価格の減少が大きくなるということです。
ベガ
ベガは、インプライドボラティリティが変動した際に、オプション価格がどれだけ変化するかを表す指標です。
計算式:ベガ = オプション価格の変化額 ÷ 原資産のボラティリティの変化
満期までの日数が長いオプションの方が、ボラティリティの影響を強く受けるため、ベガの値は大きくなります。
逆に言えば、ベガの値が小さいものを選べば、ボラティリティの影響は少ないということです。
ロー
ローは、金利の変化により、オプション価格がどれだけ変化するかを表す指標です。
計算式:ロー = オプション価格の変化額 ÷ 短期金利の変化幅
上式から分かる通り、オプション価格の変動リスクを減らしたければ、金利の変化幅とローの数値が小さいものを選ぶべきと言えるでしょう。
まとめ:ボラティリティが大きいほど見通しが立てにくくなる!
本記事では、インプライドボラティリティと、その理論について、以下のポイントを中心に解説しました。
- インプライドボラティリティとは
- 理論価格とボラティリティについて
- 理論価格の計算方法(ブラックショールズ方程式)
- リスク管理の重要性とリスクファクター
最近では、IG証券の「ノックアウトオプション」の影響もあり、為替とオプション取引を組み合わせるサービスも増え始めています。
その際は、オプション価格が発生することになりますが、本記事で紹介した通り、相場が乱高下する渦中においてはコストが高くなるということを覚えておきましょう!
以上、参考にしていただければ幸いです。




